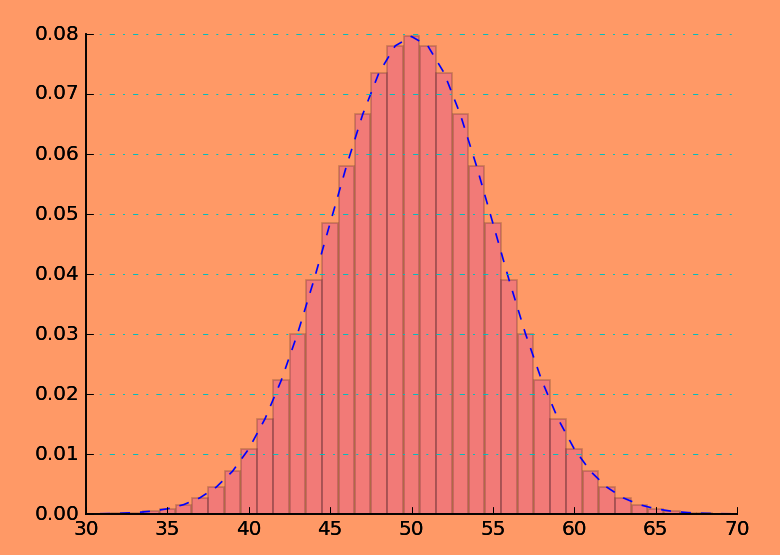
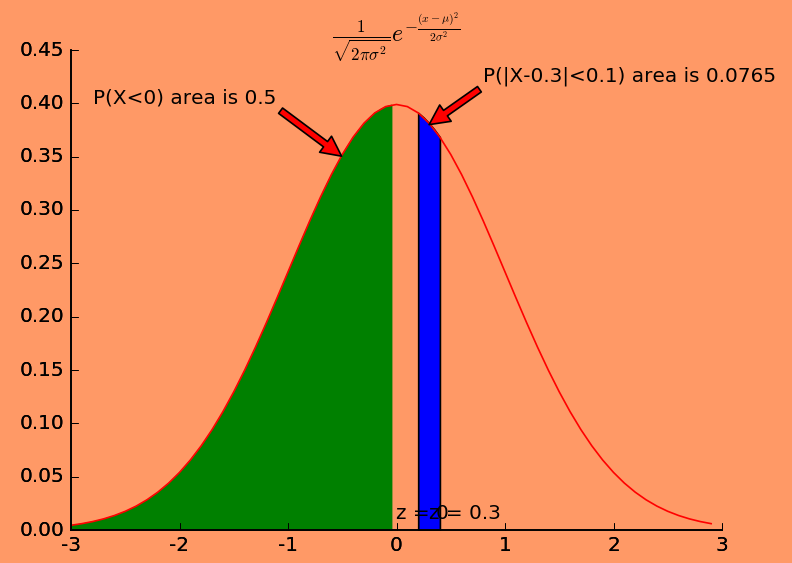
二项分布
看一下掷硬币的问题
掷一次硬币正面或者反面发生的概率都是$\frac{1}{2}$
掷五次硬币或者一次掷五个硬币(每个硬币正反 独立的,每次硬币独立的,怎么操作都一样.),记出现正面的数量为$X$.
$P(X=0)$(出现正面为0次的概率,也就是五次全为反面)?
全为反面只有一种情况,就是第一次投掷为反,第二次为反...
$$P(X=0)=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{32}$$
$P(X=1)$(出现正面为1次的概率)?
正面为1次有5种情况,就是第一次投掷为正,其他全为反;第二次为正,其他全为反...
每中情况都是$\frac{1}{32}$(出现正面的次数和非正面的次数都是$\frac{1}{2}$)
$$P(X=1)=5 \times \frac{1}{32} = \frac{5}{32}$$
$P(X=2)$(出现正面为2次的概率)?
还要枚举吗?好像有点累
分析一下:
- 先确定一个正面发生的位置,它有5种(第一次投掷为正,第二次为正...),再确定第二个正面发生的位置,第一个记录已经占走了一个位置,还有四个位置选一个为正,有4种. $5 \times 4$
- 刚刚我们先确定了,再确定,多做了排序,也就是同样第二次和第三次为正,但是我们却在刚刚把它记为了两种情况(先找到2位再发现3,和先找到3再发现2)我们要排除我们不必要的排序. $\frac{5 \times 4}{2}$
- 每中情况都是$\frac{1}{32}$
$$P(X=2)=\frac{5 \times 4}{2} \times \frac{1}{32} = \frac{5}{16}$$
$P(X=3)$?
- 确定第一个(5个位置选1个),第二个(4个位置选1个),第三个(3个位置选1个)$5 \times 4 \times 3$
- 排除不必要的排序(3个的排序为$3 \times 2$). $\frac{5 \times 4 \times 3}{3 \times 2}$
- 每中情况都是$\frac{1}{32}$
$$P(X=3)=\frac{5 \times 4 \times 3}{3 \times 2} \times \frac{1}{32} = \frac{5}{16}$$
$P(X=4)$?
- $A_5^4 = 5 \times 4 \times 3 \times 2$
- $\frac{A_5^4}{A_4^4} = \frac{5 \times 4 \times 3 \times 2}{4 \times 3 \times 2}$
- $\frac{1}{32}$
$$P(X=4)=\frac{5 \times 4 \times 3 \times 2}{4 \times 3 \times 2} \times \frac{1}{32} = \frac{5}{32}$$
$P(X=5)$?
$$P(X=5)=C_5^5 \times \frac{1}{32} = \frac{1}{32}$$
也可以把5次为正理解为0次为反,正反概率相等,那么$P(X=5)=P(X=0)$
二项分布就是重复n次独立的伯努利试验.
伯努利实验:在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变
博主个人能力有限,错误在所难免.
如发现错误请不要吝啬,发邮件给博主更正内容,在此提前鸣谢.
Email: JentChang@163.com (来信请注明文章标题,如果附带链接就更方便了)
你也可以在下方的留言板留下你宝贵的意见.