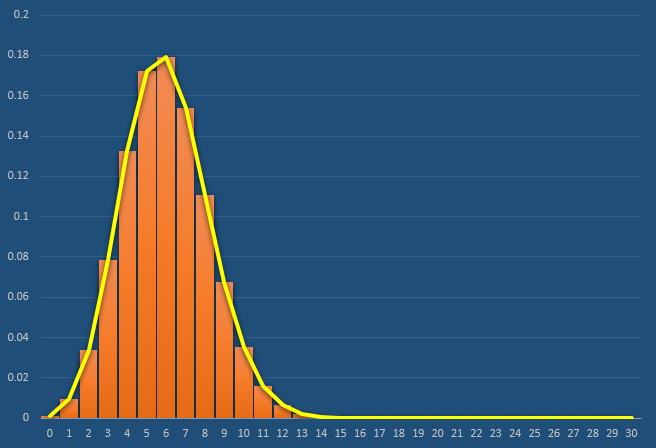
二项分布
来看上一节留下的公式
$$P(X=k) = (_k^n)p^k(1-P)^{n-k}$$
可能已经明白了二项系数$(_k^n)$什么意思,这里说一下为什么是概率是$p^k(1-P)^{n-k}$.
可能硬币事件的两种结果让我记住了$\frac{1}{2}$,那是一个比较特殊的情况.如果把事件转换为掷筛子呢?它就不再是$\frac{1}{2}$,$\frac{1}{2}$.
掷筛子有6种可能的结果,怎么会是二项分布?我没有搞混,那可能是被掷硬币这样的事件给惯性思维了,非要寻找和它一样特征的.我们要学会如何转换,把事件转变为我们常见的分布.
如果问题转换为掷筛子,点数为1或者2则甲胜出,点数为3或者4则乙胜出,点数为5或者6则丙胜出,现在寻找在n次实验中,甲胜出X次的概率?
只关心甲的概率,只需知道是甲赢了,还是输了,并不关心乙或者丙赢了他.现在就是二项分布了,甲赢(点数为1或2),甲不赢(点数不为1或2,即为3,4,5,6).则事件发生的概率分别为甲赢$\frac{1}{3}$,甲不赢$\frac{2}{3}$.
注意二项分布的特点,每次投掷都是独立的,不受之前实验的影响,每次结果都是甲赢$\frac{1}{3}$,甲不赢$\frac{2}{3}$.
那么求$P(X=0)$,假设投掷了8次:
- 通过上一节我们知道系数$(_0^8)$
- 甲赢的次数为0,那么这种可能就是全输的概率,就是每次概率是$\frac{2}{3}$,则$p=(\frac{2}{3})^8$
- $P(X=0)=(_0^8) \times (\frac{2}{3})^8$
$P(X=1)$:
- 系数$(_1^8)$
- 甲赢的次数为1,那么这种可能就是1次为胜,7次为输的概率.即8次事件中,发生了1次概率是$\frac{1}{3}$事件和$(8-1)$次概率为$\frac{2}{3}$事件,则概率为$p=(\frac{1}{3})^{1} \times (\frac{2}{3})^{8-1}$
- $P(X=1)=(_1^8) \times (\frac{1}{3})^{1} \times (\frac{2}{3})^{8-1}$
$P(X=2)$:
- 系数$(_2^8)$
- 发生了2次概率是$\frac{1}{3}$事件和$(8-2)$次概率为$1-\frac{1}{3}$事件(两种结果,总的概率为1),则
$p=(\frac{1}{3})^{2} \times (1-\frac{1}{3})^{8-2}$ - $P(X=2)=(_2^8) \times (\frac{1}{3})^{2} \times (1-\frac{1}{3})^{8-2}$
沿着这个方法走下去,就会发现如何去利用公式了.
可汗公开课里面可能不是这样讲的,但是意思都是一样的.老师是一个投篮的例子.我只是想让你更名明白,不一定需找只有2种结果的事件(篮球不关注几分球也是这个意思),可以转变为发生或不发生(这样就是两种结果了).我表达的不是很好,不过看完这个例子应该可以明白想表达的意思.
博主个人能力有限,错误在所难免.
如发现错误请不要吝啬,发邮件给博主更正内容,在此提前鸣谢.
Email: JentChang@163.com (来信请注明文章标题,如果附带链接就更方便了)
你也可以在下方的留言板留下你宝贵的意见.