置信区间例题
In a local teaching district a technology grant is available to teachers in order to install a cluster of four computers in their classrooms. From the 6250 teachers in the district, 250 were randomly selected and asked if they felt that computers were an essential teaching tool for their classroom. Of those selected,142 teachers felt that computers were an essential teaching tool.
某地区教学区获得一批技术拨款,用于在教师中安排4台一组的计算机.该区总共有6250名教师,随机抽取250名,并且问他们是否认为计算机是教师必备的教学工具.抽取的教师中,有142名认为计算机是教学必备的工具.
问题1:
计算一个99%置信区间,其中教师认为计算机是必备的教学工具.
定义1表示计算机被认为是必备工具,占比为p,0表示计算机被认为不是必备工具,占比为q=1-p.
$\bar{x} = \frac{1\times 142 + 0 \times 108}{250} = 0.568$
$S^2 = \frac{142\times (1-0.568)^2 + 108\times (0-0.568)}{250-1}=0.246$
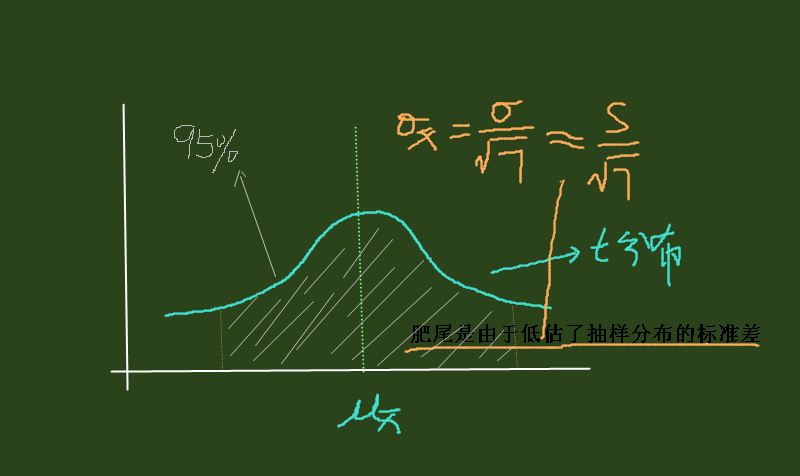
$\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{250}} \approx \frac{S}{\sqrt{250}} = 0.031$
这里需要用到z表格
z表格的值应该为0.99/2+0.5=0.995
对应2.58个标准差处
大概99%的概率,样本均值在抽样分布均值左右2.58个标准差范围.
$0.568 \pm 2.58 \times 0.031 = 0.568 \pm 0.08$
0.488-0.648
问题2:
保持99%置信水平的前提下,如何缩小置信区间?
抽取更大的样本.
博主个人能力有限,错误在所难免.
如发现错误请不要吝啬,发邮件给博主更正内容,在此提前鸣谢.
Email: JentChang@163.com (来信请注明文章标题,如果附带链接就更方便了)
你也可以在下方的留言板留下你宝贵的意见.