概率密度函数
首先我们需知道随机变量所有值发生概率和等于1
概率密度函数是对连续随机变量而言的.
对于连续随机变量,我们很难说$P(X=0)$(X为0的概率)是多少,而且这是个很难测的数值,因为这里不是说的0.00001,也不是-0.0000001,就是0.
所以对密度函数的概率描述是$P(|X-0.3|<0.1)$才是比较合理的,也就是你要指的是一个值的区间(结果落在这个区间的概率),而不是一个确定的值(这样是没有意义的).
图中阴影部分有点问题,并没有填充到0,但是概率计算取到了,这个我在代码中对应位置解释了,图就讲究用吧,你明白我的意图就行了.
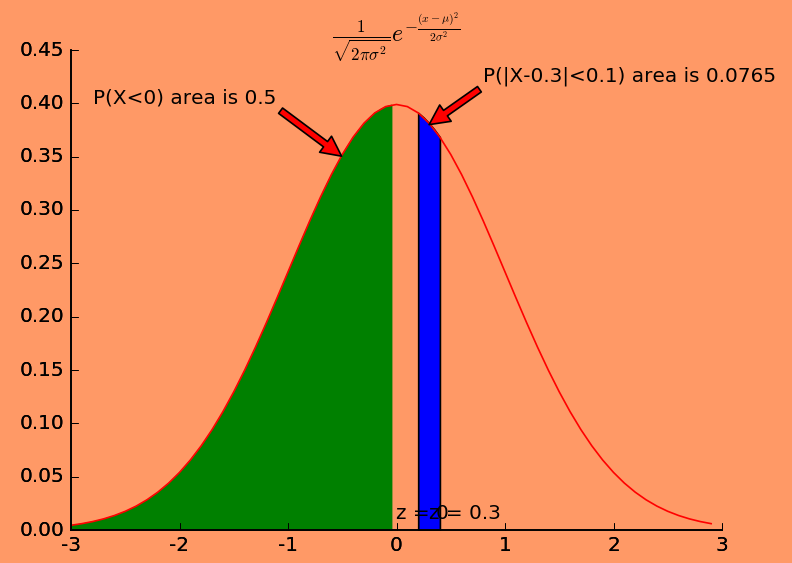
图片的密度函数是标准的正态分布函数
我们不能说$P(X=0)=0.4$,而是$P(X \leqslant 0)=0.5$就会比较合理
观察密度函数的图,面积才是表示密度函数的概率值.而不是x对应y坐标.
你也可以用它的累积函数画出对应的线图,在学习正态分布的时候我会把他们画在一起的.(这里没有采用积分,只是自己定义了一个循环累积代替了累积函数.)
假设曲线为$f(x)$,概率是面积,也就是对函数$f(x)$的积分.
$$P(0.1<X<0.2) = \int_{0.1} ^{0.2} f(x)d(x)$$
其中
$$\int_{-\infty} ^{\infty} f(x)d(x)=1$$
看到这个公式,你应该明白了,对于连续随机变量,我们寻找它确定值的发生概率几乎等于0,从图中也可以发现,它只会是一根线段,围不成一个面.
密度函数图示代码:
import numpy as np
from scipy import exp, sqrt, stats
import matplotlib.pyplot as plt
from mpl_toolkits.axisartist.axislines import SubplotZero
import pandas as pd
def fun(t):
return stats.norm.pdf(t,)
x = np.arange(-3, 3, 0.1)
xticks = np.arange(-3, 3.1, 1)
yticks = np.arange(0, 0.55, 0.05)
# 设置支持中文
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False
fig = plt.figure(figsize=(7, 5), dpi=120, facecolor='#FF9966', edgecolor='c')
ax1 = SubplotZero(fig, 1, 1, 1, axisbg='#FF9966')
fig.add_subplot(ax1)
# ax1.grid(True, color='k', linestyle='-.')
ax1.axis['right', 'top'].set_visible(False)
ax1.set_yticks(yticks)
ax1.set_xticks(xticks)
ax1.set_ylim(0, 0.45)
ax1.set_xlim(-3, 3)
# 绘制密度函数
ax1.plot(x ,fun(x), 'r')
# 标题的内容实际是一个公式,如果你想尝试用代码写公式,可以参考latex规范.
ax1.set_title(r'$\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$')
# 绘制概率发生区间1
z = 0.3
x2 = np.arange(z-0.1, z+0.1, 0.05)
sum = 0
delta = 0.001
s = np.arange(z-0.1, z+0.1, delta)
for i in s: # 计算累积
sum += fun(i) * delta
ax1.fill_between(x2, fun(x2))
ax1.annotate(
'P(|X-%s|<=0.1) area is '%z + str(round(sum, 4)), xy=(0.3, 0.38), xytext=(0.8, 0.42),
arrowprops=dict(facecolor='red', shrink=0.001)
)
ax1.annotate(
'z = ' + str(z), xy=(z, 0.01)
)
# 绘制概率发生区间2
z = 0
x2 = np.arange(-4, z, 0.05) # z应该加一个小于等于0.05的数,这是我的疏忽,你发现图上并没有填充到0,那是因为arange不能取到z值.在下面计算的时候我取到了,它的结果是对的
sum = 0
delta = 0.0001
s = np.arange(-4, z+delta, delta)
for i in s:
sum += fun(i) * delta
ax1.annotate(
'P(X<=%s) area is ' % z+ str(round(sum, 4)), xy=(-0.5, 0.35), xytext=(-2.8, 0.4),
arrowprops=dict(facecolor='red', shrink=0.01)
)
ax1.annotate(
'z = ' + str(z), xy=(z, 0.01)
)
ax1.fill_between(x2, fun(x2), color='g')
plt.show()
离散的随机变量概率图
下面是一个离散随机变量的概率分布,但是我们不能说是密度函数,它的值是一个个枚举出来的
这是一个掷筛子的概率,但是这是一个处理过的筛子,它的二被改成了六
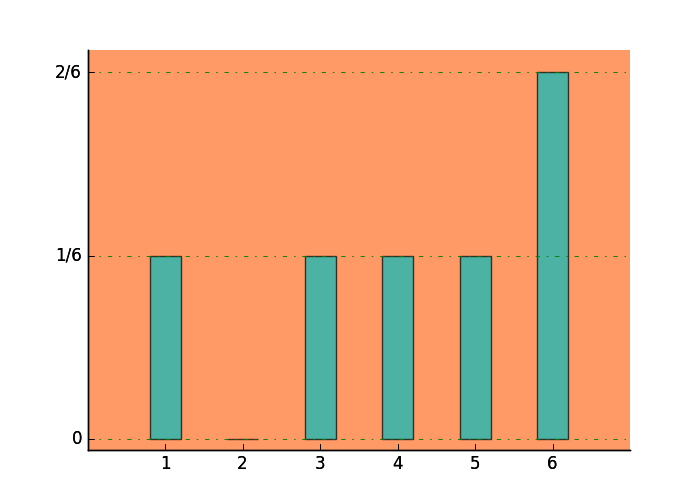
$\frac{1}{6}+0+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{2}{6}=1$
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axisartist.axislines import SubplotZero
import pandas as pd
x = np.array([1, 2, 3, 4, 5, 6])
y = np.array([1/6, 0, 1/6, 1/6, 1/6, 2/6])
xticks = np.arange(1, 7, 1)
yticks = ['0', '1/6', '2/6']
fig = plt.figure(figsize=(7, 5), dpi=120, facecolor='#FF9966', edgecolor='c')
ax1 = SubplotZero(fig, 1, 1, 1, axisbg='#FF9966')
fig.add_subplot(ax1)
ax1.grid(axis='y', color='g', linestyle='-.')
ax1.axis['right', 'top'].set_visible(False)
plt.yticks((0, 1/6, 2/6), yticks)
plt.xticks(xticks)
plt.xlim(0, 7)
plt.ylim(-0.01, 2/6+0.02)
width = 0.4
ax1.bar(x-width/2, y, width, color='c', alpha=0.7)
plt.show()
博主个人能力有限,错误在所难免.
如发现错误请不要吝啬,发邮件给博主更正内容,在此提前鸣谢.
Email: JentChang@163.com (来信请注明文章标题,如果附带链接就更方便了)
你也可以在下方的留言板留下你宝贵的意见.



