统计学28：正态分布Excel练习

统计学•目录 统计学•类别 math

---

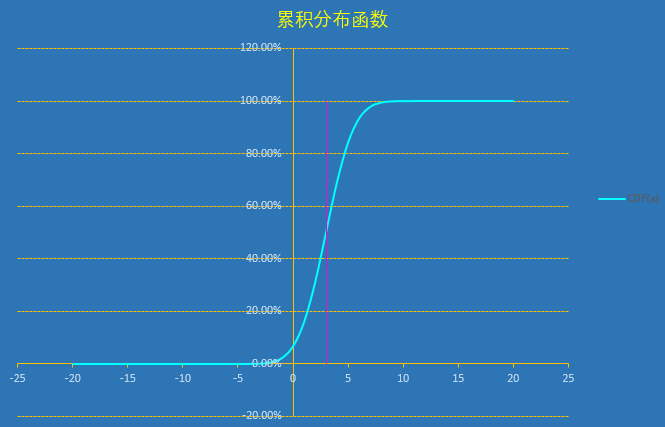
正态分布Excel练习

他有很多个名字：正态分布，高斯分布，钟形曲线

正态分布密度函数

$$P(X) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\big(\frac{x-\mu}{\sigma} \big)^2}$$

标准z分数$\frac{x-\mu}{\sigma}$ 离均值的距离除以标准差（离均值有多少个标准差远）

二项分布与正态分布的比较

试验次数	10
左移步数平均值	5
方差	2.5
标准差	1.581

结束位置	左	右	二项分布	正态分布
10	0	10	0.000976563	0.001700073
8	1	9	0.009765625	0.010284844
6	2	8	0.043945313	0.0417071
4	3	7	0.1171875	0.113371653
2	4	6	0.205078125	0.206576621
0	5	5	0.24609375	0.252313254
-2	6	4	0.205078125	0.206576621
-4	7	3	0.1171875	0.113371653
-6	8	2	0.043945313	0.0417071
-8	9	1	0.009765625	0.010284844
-10	10	0	0.000976563	0.001700073

表格中的计算可以去下载表格，点几下你就明白了．建议更改实验次数观察图像变化．

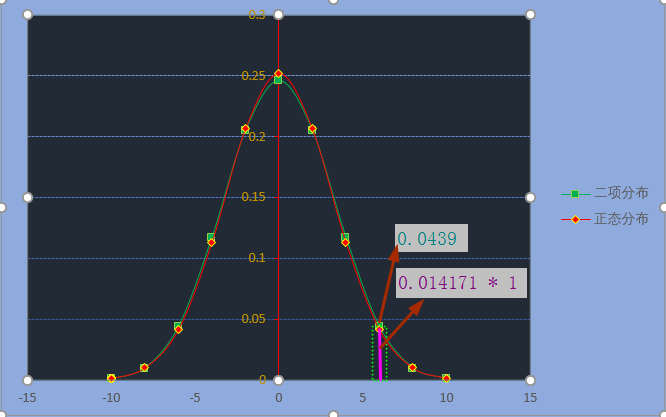
在Excel中，上图是散点图选项中散点图与平滑曲线，它并不是使用折线图的选项绘制的．

之前的文章已经解释了离散变量和连续变量．对于二项分布，它描述的离散情况，对应的概率$P(X=2)=0.0439$（左移两步的概率）离散变量可以一一枚举，而连续变量我们说$P(X=2)$几乎为0，因为很难取到刚刚好的值．在这里我们看到正太分布$P(X=2)$对应的为0.04171（密度函数的值），它其实是我们假设位置在5.5步到6.5步，也就是设宽度为1单位乘以对应的高．所以在图上我标记了一根线段，它的面积为$0.04171\times 1$（实际我们应该求积分的），对于二项分布，它表示是一个条形图的高，我用绿色的框标识了出来．

收敛情况

总移步数	10	20	30	40	50	60
右移步数	10	15	20	25	30	35
左移步数	0	5	10	15	20	25
二项分布概率	0.000976563	0.014785767	0.027981601	0.036584738	0.041859149	0.045029465
左移步数平均值	5	10	15	20	25	30
方差	2.5	5	7.5	10	12.5	15
正态分布	0.001700073	0.014644983	0.027514099	0.036144479	0.04151075	0.044766421
差值	0.000723511	0.000140784	0.000467501	0.000440259	0.000348399	0.000263044

有必要来练习一下正态分布函数的计算：
计算表中第二列为例
$$P(X＝5) = \frac{1}{\sqrt 5 \sqrt{2\pi}}e^{-\frac{1}{2}\big(\frac{5-10}{\sqrt 5} \big)^2}=0.014644983$$

表格中的计算可以去下载表格，它在同一个excel文件中名为＇收敛＇的表格．

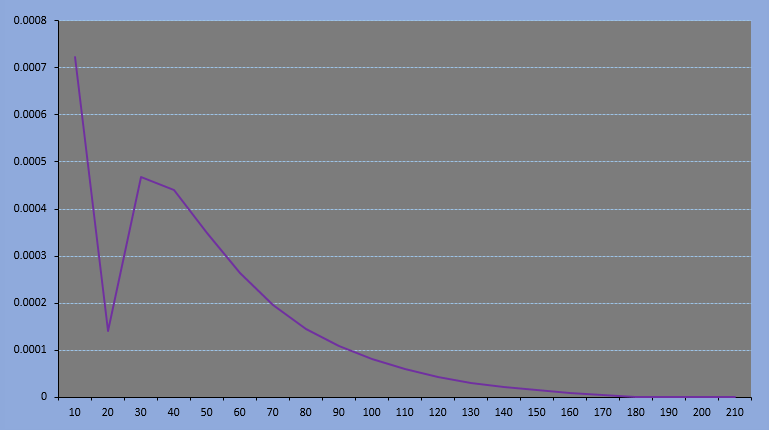
随着总的移动步数（实验样本的容量）增加，他们的差是趋于0的．

在电子表格中调节最终位置观察图像时，注意不能为奇数，原因是非左即右，步差为偶数．奇数是不收敛的，你可以尝试一下不收敛的图像是什么样子．（收敛其实就是随着变量的变化，结果趋向于某一个值．）

---

本节excel文件下载链接

中文表格
可汗学院原表格

---

博主个人能力有限，错误在所难免．
如发现错误请不要吝啬，发邮件给博主更正内容，在此提前鸣谢．
Email: JentChang@163.com （来信请注明文章标题，如果附带链接就更方便了）
你也可以在下方的留言板留下你宝贵的意见．