误差范围
情景:统计一个总体的投票情况,这里有两个候选人A and B
结果:B的票数占总的比例是p,则A的票数占比是1-p
为了计算方便,我们把A记为0,把B记为1
这是一种二进制编码的思想,在计算机应用中经常会用到.
则均值为(它是一个分布取不到的值)
$\mu = p$
但是p是很难去一一统计然后得出的.不可能把每个人都去调查一遍的.
抽样
随机选取一部分,100人吧
其中57人选A, 43人选B.
$$\bar{x}=\frac{57\times 0 + 43\times 1}{100} = 0.43$$
$$S^2 = \frac{57\times (0-0.43)^2 + 43\times (1-0.43)^2}{100-1} = 0.2475$$
$$S = \sqrt{0.2475} = 0.50$$
样本的离均值平方对n-1个求期望,是对总体无偏差估计
思考:这个样本估计总体,那它有多少可信度,也就死有多好的去估计呢
均值的最好估计为
均值0.43意味着43%的人投B
在0.43周围的存在?一个区间,我们有?确信真实均值是在该区间内的.
原分布是一个离散分布,我们从总体中,随机抽100个求均值,不断的抽取.这其实就是一个样本均值抽样分布.
样本均值抽样分布的标准差估为0.05(5%),(这在之前是有过计算过程的,看图应该可以明白.)
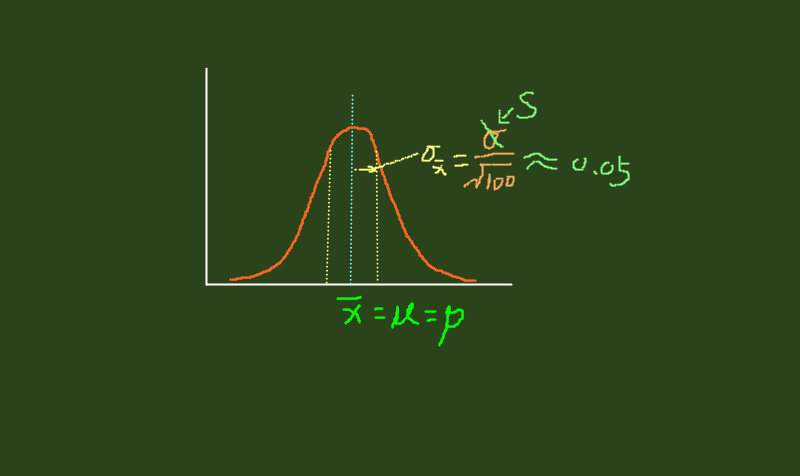
有95%的机率合理确信总体的真实均值p在?此区间内
下一节继续.这里理解把问题研究对象转换成了一个样本均值抽样分布.
博主个人能力有限,错误在所难免.
如发现错误请不要吝啬,发邮件给博主更正内容,在此提前鸣谢.
Email: JentChang@163.com (来信请注明文章标题,如果附带链接就更方便了)
你也可以在下方的留言板留下你宝贵的意见.



