二项分布的期望值

假设随机变量X表示n次实验的次数，其中每次成功的概率是P.

$$E(X) = np$$

在二项分布中，期望值可以看成是最可能得到的那个结果．

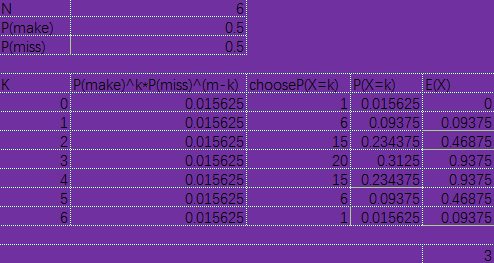
假设投篮的命中概率为40％，投10次．
那么$E(X) = np = 10 \times 40\% =4$

可以理解为命中概率为40％，那么投10次，可能4次命中．

回顾二项式概率的公式：

$$P(X=k) = (_k^n)p^k(1-P)^{n-k}$$

期望值公式：

$$E(X) = \sum_{k=0}^nkP(X=k)=\sum_{k=0}^n(_k^n)kP^k(1-P)^{n-k}$$
$　　E(X) =0(_0^n)p^0(1-P)^{n-0}+1(_1^n)p^1(1-P)^{n-1}+…+n(_n^n)p^n(1-P)^{n-n}\\
　　　　　=1(_1^n)p^1(1-P)^{n-1}+…+n(_n^n)p^n(1-P)^{n-n} \\
　　　　　=\sum _{k=1}^n(_k^n)P^k(1-P)^{n-K}
$

代入二项式系数公式
$$二项式系数　　　(_k^n)=\frac{n!}{k!(n-k)!}$$
　　　　　　　　　$E(X) =\sum _{k=1}^n \frac{n!}{k!(n-k)!} k P^k(1-P)^{n-K}\\
　　　=\sum _{k=1}^n \frac{n!}{k(k-1)!(n-k)!} k P^k(1-P)^{n-K}\\
　　　=\sum _{k=1}^n \frac{n!}{(k-1)!(n-k)!} P^k(1-P)^{n-K}\\
　　　=\sum _{k=1}^n \frac{n(n-1)!}{(k-1)!(n-k)!} PP^{k-1}(1-P)^{n-K}\\
　　　=np\sum _{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!} P^{k-1}(1-P)^{n-K}\\
$

令$a=k-1,b=n-1$，则$n-k=b-a$
　　　　　　　　　$E(X) =np\sum _{a=0}^b \frac{(b)!}{a!(b-a)!} P^{a}(1-P)^{b-a}\\
　　　=np\sum _{a=0}^b (_a^b) P^{a}(1-P)^{b-a}\\
　　　= np
$